57
CRITERIO DE LA CAÍDA DE TENSIÓN
La caída de tensión entre fases en alterna trifásica responde a la ecuación siguiente:
Sabemos que...
D
U(%)
= X 100
P = S·cos
j
= 2520 x 0,8 = 2016 kW
tg
j
= 0,75
U = 25 kV
Ahora necesitamos calcular R y X.
Para el valor de la temperatura máxima considerada (70 ºC) podemos obtener el valor de R aplicando la fórmula de variación de la
resistencia con la temperatura:
R
70 ºC LA-56
= R
20 ºC LA-56
·(1+
a
·(70-20))·L = 0,6136 x (1+0,00403 x (70-20)) x 20 = 14,74
W
R
20ºC
se obtiene de la tabla de datos de los conductores desnudos y el valor de variación de la resistencia específica por temperatura del
conductor
a
es igualmente un dato conocido.
Para obtener la reactancia aplicamos la siguiente fórmula:
X =
w
L = 2 x
p
x 50 x (0,5+4,6 x log(DMG/r)) x 10
-4
x L
Donde DMG es la distancia media geométrica en mm, r el radio del conductor en mm y L es la longitud de la línea en km.
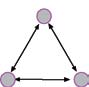
DMG = (a
12
·a
13
·a
23
)
1/3
En nuestro caso las 3 distancias son iguales y por tanto DMG = 1,2 m.
El radio del conductor r es 9,45/2 mm (ver tabla).
Y la longitud de la línea L es de 20 km.
X
LA-56
=
w
L = 2 x
p
x 50 x (0,5+4,6 x log(3000/90)) x 10
-4
x 20 = 7
,26
W
Ahora ya podemos obtener la caída de tensión:
D
U(%)
LA56
= x
100
= x
100 = 6,51%
Tomando valores de la tabla de datos de los cables y sustituyendo en las fórmulas:
R
70 ºC LA-110
= R
20 ºC LA-110
(1 +
a
(70-20))·L = 0,3066 x (1+0,00403 x (70-20)) x 20 = 7
,36
W
X
LA-110
=
w
L = 2 x
p
x 50 x (0,5+4,6 x log(3000/(14/2))) x 10
-4
x 20 = 6,77
W
D
U(%)
LA-110
= x
100
= x
100 = 4,01%
P(R + Xtg
j
)
U
2
1
2
3
a
23
a
13
a
12
P(R + Xtg
j
)
U
2
2016000x (14,74 + 7
,26 x 0,75)
25000
2
P(R + Xtg
j
)
U
2
2016000x (7,36 + 6,77 x 0,75)
25000
2
H)
EJEMPLOS DE CÁLCULO